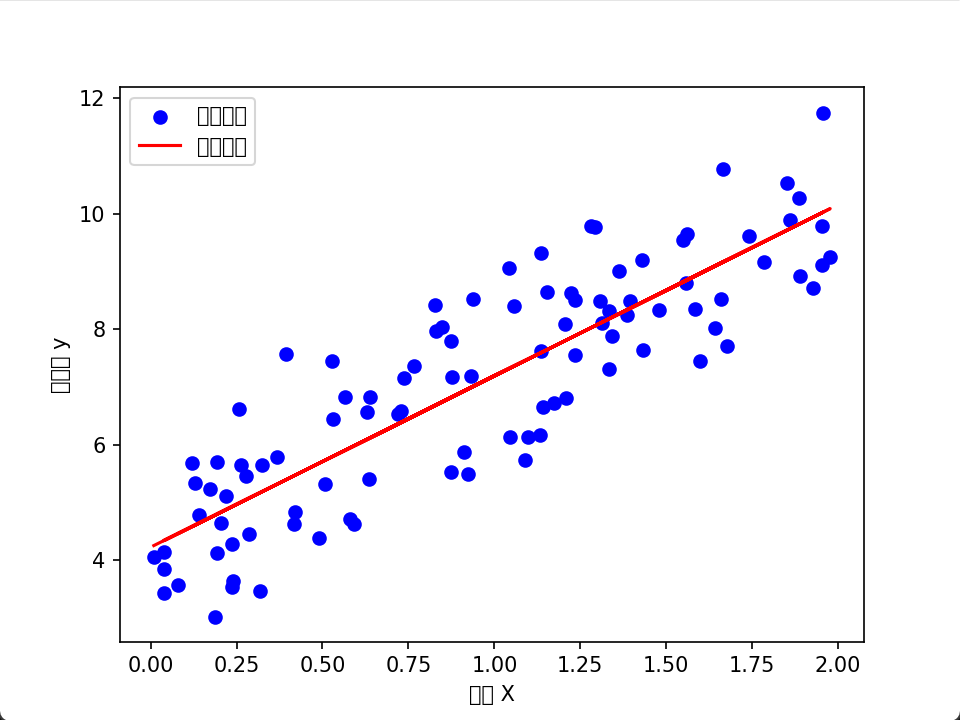
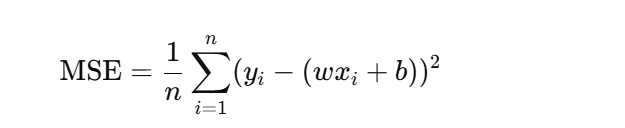线性回归是机器学习中的常见算法，前些日子一直在看相关的数学知识，这次决定在AI的帮助下，用python实现一次线性回归算法。这里用均方误差公式函数配合梯度下降法，试图拿下这个东西。

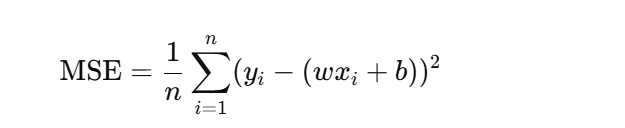
image-20251130171047684

线性回归你的目的是找到一个形似y=wx+b的公式，w是权重，b是偏置。

第一步，先提供一个基础模板

1
2
3
4
5
6
7
import numpy as np
import matplotlib.pyplot as plt
#生成示例数据
np.random.seed(1)
x=np.random.rand(100,1)
#生成目标值，同时加上一些噪声数据
y=4*x+3+np.random.randn(100,1)

第二步，我们写一个类，实现线性回归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class LinearRegression:
    def __init__(self, learning_rate=0.01, iterations=1000):
        self.learning_rate = learning_rate
        self.iterations = iterations
        # 定义权重和偏置
        self.w = 0  # 使用 self 来定义实例变量
        self.b = 0  # 使用 self 来定义实例变量

    def fit(self, x, y):
        # 样本容量
        m = len(x)
        for _ in range(0, self.iterations):
            y_pred = self.predict(x)  # 调用正确的预测方法
            error = y - y_pred
            # 计算梯度
            dw = (2 / m) * np.dot(x.T, error)  # 对 w 求偏导
            db = (2 / m) * np.sum(error)  # 对 b 求偏导

            # 更新权重和偏置
            self.w -= self.learning_rate * dw
            self.b -= self.learning_rate * db

    def predict(self, x):
        # 返回预测值
        return self.w * x + self.b  # 使用正确的 self 引用

最后一步，让数据可视化

1
2
3
4
5
6
7
# 绘制结果
plt.scatter(X, y, color='blue', label='真实数据')
plt.plot(X, model.predict(X), color='red', label='拟合直线')
plt.xlabel('特征 X')
plt.ylabel('目标值 y')
plt.legend()
plt.show()

借助AI，理清楚思路，首先梯度的计算是借助一个循环进行的，循环次数是我们自己设定。求偏导就是得到的参数，

或者用已有的python库：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

# 1. 复用上面的模拟数据（x, y）
# 2. 创建并训练模型
model = LinearRegression()
model.fit(x, y)  # 训练模型

# 3. 获取模型参数
w_sklearn = model.coef_[0][0]  # 权重
b_sklearn = model.intercept_[0]  # 偏置
print(f"sklearn实现的权重w: {w_sklearn:.4f}, 偏置b: {b_sklearn:.4f}")

# 4. 预测
y_pred_sklearn = model.predict(x)

# 5. 模型评估
mse = mean_squared_error(y, y_pred_sklearn)  # 均方误差
r2 = r2_score(y, y_pred_sklearn)  # 决定系数（越接近1越好）
print(f"均方误差(MSE): {mse:.4f}")
print(f"决定系数(R²): {r2:.4f}")

# 6. 可视化结果
plt.scatter(x, y, label='真实数据', alpha=0.6)
plt.plot(x, y_pred_sklearn, color='green', label=f'拟合直线: y={w_sklearn:.2f}x+{b_sklearn:.2f}')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.title('sklearn实现线性回归')
plt.show()

结果如图所示
image-20251130191248947